정렬 리스트
데이터가 특정 기준으로 정렬되어있는 리스트이다. 예를 들면 정수형 리스트인 경우 오름차순 or 내림차순으로 정렬되어 있다면 정렬리스트이다.
정렬이 되어 있기 때문에 시간복잡도면에서 비정렬 리스트보다 효율적이다.
예를 들어 리스트에서 아이템을 찾아주는 함수의 시간복잡도를 살펴보자면 정렬 리스트가 binary search로 구현된 경우, 시간 복잡도는 O(logN)이지만 비정렬 리스트는 시간 복잡도가 O(N)이다.
|
search 함수 |
정렬 리스트 (2진 탐색) |
비정렬 리스트 |
|
시간 복잡도 |
O(logN) |
O(N) |
정렬리스트를 구현하는 방식도 다양하다. 일단 여기서는 2진 탐색을 기준으로 설명하겠다.
Binary Search (2진 탐색)
2진 탐색은 정렬이 된 자료를 반으로 나누어 가며 검색을 하는 알고리즘이다.
오름차순으로 정렬된 자료에서만 사용 가능하며 기본 코드 구성은 다음과 같다
int main() {
int length = 5;
int arr[5] = { 1,2,3,4,5 };
int start = 0; // 배열의 시작 index
int end = length - 1; // 배열의 마지막 index
int item; // 비교할 데이터
bool find = false;
while (start <= end && !find) {
int mid = (start + end) / 2;
if (arr[mid] < item) {
start = mid + 1;
}
else if (arr[mid] > item) {
end = mid - 1;
}
else {
find = true;
}
}
}
이진 탐색의 포인트는 mid 값을 조정을 한다는 것이다. 리스트는 오름차순으로 정렬되어있다고 한다.
리스트에서 찾고자 하는 값이 arr[mid] 보다 크다면 어짜피 mid 앞 쪽에 위치한 데이터에는 찾고자 하는 값이 없을 것이다. 왜냐면 정렬이 된 상태이기 때문이다. 그래서 아예 찾고자 하는 데이터의 시작위치인 start 값을 mid+1 을 시켜서 arr[mid] 보다 뒤에 위치한 데이터에서 또 값을 찾는다.
찾고자 하는 값이 arr[mid]보다 작은 경우에도 이 논리는 마찬가지로 적용된다. arr[mid]보다 작은 경우 어짜피 mid 뒤 쪽에 위치한 데이터에는 값이 없을 것이므로 end 값을 mid-1을 해서 arr[mid]보다 앞 쪽에 위치한 데이터들을 살핀다.
이를 반복하다 보면 처음에는 분명 start<end 인 상태에서 출발해서 start>end 인 순간이 온다. 이 때부터는 리스트에 찾고자 하는 값이 없다는 뜻이므로 while 문의 조건으로 start<=end를 걸어준다.
Binary Search 알고리즘 시간 복잡도
알고리즘에서 가장 중요한 시간 복잡도를 big o notation으로 알아보겠다.
처음에 리스트에 N개의 데이터가 있다고 하면, 맨 처음 이진 탐색을 진행하면 N/2 의 데이터가 남을 것이다.
두번째로 이진 탐색을 진행하면 첫번째로 진행하고 남은 데이터인 N/2 의 반이 남을 것이다. 즉 N/2 X 1/2
세번째로 이진 탐색을 진행하면 또 마찬가지로 N/2 X 1/2 X 1/2
이를 통해 이진 탐색을 K번 진행하면 남아 있는 데이터는
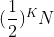
이 된다.
이렇게 이진 탐색을 진행했을 때 worst case는 데이터가 1개가 남을 때까지 진행하는 것인데, 이 경우 저 값은

1에 거의 근접하게 된다.
양변에 2의 K제곱을 곱해주면

이다.
양변에 로그를 취해주면

이 된다.
이때 K는 데이터가 N개일 때의 시행 횟수 이므로 이진탐색의 시간복잡도는 상수를 버린 O(logN)이 된다.
Array based implement
대충 정렬 알고리즘도 봤으니 배열로 구현한 클래스를 통해 직접 보도록 하겠다.
class sorted {
public:
unsorted()
void get(int& item); //currentpos에 있는 데이터를 돌려줌
void reset(); // currentpos를 초기화 시킴
void insert(int item);
void deleted(int item);
bool full() const;
void retrieve(int& item, bool& find); // 아이템이 리스트에 있는지 확인
private:
int currentpos; // 리스트에서 현재 보고있는 위치를 알려줌
int items[MAX];
int len; // 데이터의 길이
};나머지 쉬운 함수들은 넘어가고 오늘은 insert deleted 만 보도록 하겠다. 나머지는 비정렬 리스트와 비슷하게 진행된다.
-
insert(int item)
void insert(int item) {
bool find = 0;
int start = 0;
int end = len - 1;
int mid;
while (start <= end && !find) {
mid = (start + end) / 2;
if (items[mid] < item) {
start = mid + 1;
}
else if (items[mid] > item) {
end = mid - 1;
}
else {
find = 1;
}
}
for (int i = len; i > mid; i--) {
arr[i] = arr[i - 1];
}
arr[mid] = item;
len++;
}이진 탐색을 이용해서 구현해봤다. 중복된 값이 있어도 ㅇㅋ
-
deleted(int item)
void deleted(int item) {
void insert(int item) {
bool find = 0;
int start = 0;
int end = len - 1;
int mid;
while (start <= end && !find) {
mid = (start + end) / 2;
if (items[mid] < item) {
start = mid + 1;
}
else if (items[mid] > item) {
end = mid - 1;
}
else {
find = 1;
}
}
if (find == 1) {
for (int i = mid + 1; i < len; i++)
arr[i - 1] = arr[i];
len--;
}
}
}이것도 이진탐색으로 구현했다.
Linked List implement
연결 리스트로 정렬 리스트를 구현하는 것은 약간 까다롭다. 구현의 포인트는 deleted 에서 리스트간의 연결을 유지하는 것이다. insert에서도 값이 들어갈 자리를 찾는 구현을 하는 부분도 주의 깊게 봐야한다.
class sorted {
public:
sorted();
~sorted();
void reset();
void length();
void insert(int input);
void deleted(int input);
void get(int& output);
bool full();
private:
Node* data;
Node* currentpos;
int len;
};
struct Node {
int item;
Node* next;
};포인트는 소멸자에서 할당 해제를 다 해줘야하는 부분이다.
-
~sorted 소멸자
~sorted() {
Node* node;
while (data != NULL) {
node = data;
data = data->next;
delete node;
}
len = 0;
}언제나 그랬듯이 코드의 순서가 중요하다. node 객체에 리스트 데이터를 넣고 data는 그 다음 노드를 가리키도록 한다. 그리고 node 객체를 할당해제 해준다. 길이를 0으로 만든 것도 내 마음
-
insert(int input)
void insert(int input) {
Node* location = data; // 현재 위치
Node* prelocation = NULL; // 이전 위치
bool find = 0;
while (!find) {
if (location->item < input) {
prelocation = location;
location = location->next;
find = (location == NULL);
}
else {
find = 1;
}
}
Node* node = new node;
node->item = input;
if (prelocation == NULL) {
node->next = data;
data = node;
}
else {
prelocation->next = node;
node->next = location;
}
len++;
}insert 함수의 중요성은 데이터를 추가할 때 연결리스트를 유지하는 것이다. 이를 위해서 현재위치를 기억하는 포인터(location)와 이전 위치를 기억하는 포인터(prelocation)를 총 두개를 만들었다.
제일 처음 상태에는 location에 첫번째 노드 주소를 넣는다. prelocation은 이 때 NULL이다.
그 다음, while 문을 돌면서 item이 위치한 location을 찾는다. 추가할 데이터의 값이 리스트의 값보다 작아지는 순간이 바로 input이 들어갈 위치이다. 따라서 if문에는 리스트의 값보다 작아지는 순간을 찾을 때까지 prelocation과 location을 이동시킨다. 이 때 upper limit은 location이 NULL, 즉 마지막 리스트인 경우이다.
while문을 탈출한 후 보이는 if문은 추가할 아이템이 제일 처음으로 들어가야하는 경우이다. 이때는 prelocation값이 NULL이므로 if의 조건으로 달아줬다. node 객체에 값을 넣고 data가 node를 가리키게 함으로써 제일 처음으로 연결하였다.
else문을 통해서는 나머지 상황을 처리했다. 마지막에는 len++로 리스트의 길이를 증가시켰다.
-
deleted(int input)
void deleted(int input) {
Node* location = data;
Node* prelocation = NULL;
bool find = 0; // 데이터를 찾았는지 반환
bool search = 1; // 탐색을 계속 진행할지 반환
while (!find && search) {
if (location->item == input) {
find = 1;
}
else {
prelocation = location;
location = location->next;
search = (location != NULL);
}
}
if (find == 1) {
if (prelocation == NULL) {
Node* node;
node = data;
data = data->next;
delete node;
}
else {
Node* node;
node = location;
prelocation->next = location->next;
delete node;
}
}
len--;
}이 코드의 포인트 또한 마찬가지로 연결리스트를 유지하는 것이다.
먼저 while문을 통해 삭제할 데이터가 있는 위치를 알아낸다. 이 때
if문은 삭제할 아이템이 첫번째 노드에 있는 경우이다. 이 경우는 prelocation의 값이 NULL 이므로 if의 조건으로 달아줬다. 그 후 node 의 값을 비교해가며 탐색한다. 같은 경우는 find=1을 통해 while문을 탈출하고 다음 if문으로 진행한다. 아니라면 prelocation과 location의 위치를 옮긴다. 이 때 location이 NULL, 즉 마지막 노드인 경우에는 search가 false가 되도록하여 while문을 돌지 않도록 한다.
if문에서는 insert와 마찬가지로 새 객체를 만들어서 삭제할 데이터의 위치를 넣고 이전 노드의 next를 다음다음 노드의 주소로 바꾼다. 이러면 연결리스트 완성 그리고 마지막에는 객체를 할당 해제 해준다. 이 때 삭제할 데이터가 맨 첫번째 노드에 있는 경우는 prelocation==NULL을 통해서 예외 처리했다.
-
get(int& output)
void get(int& output) {
if (currentpos == NULL)
currentpos = data;
output = currentpos->item;
currentpos = currentpos->next;
}currentpos가 NULL인 경우에는 data를 넣어주고 output에 currentpos의 데이터를 넣을 수 있도록 했다. 마무리로는 currentpos->next로 주소값을 이동시켰다.
여기까지 봤으면 생길 수 있는 질문
▶배열은 이진탐색을 쓰는데 왜 연결리스트는 이진탐색의 '이' 자도 안쓰는가?
이는 연결리스트 구현의 한계라고 볼 수 있는데 당연히 중간값을 찾는게 어렵다. 연결리스트의 중간주소? 그런게 없음
배열은 메모리상에서 가까이 옆에 붙어있음, 즉 지역성이 좋다. 하지만 연결리스트는 하나의 노드가 생겼을 때 다음 노드의 주소가 어디일지 예측을 못한다. 즉 지역성이 별로임 그래서 이는 순회시간이 더 오래걸린다는 단점으로 돌아온다. 이와 관련된 이야기는 시간복잡도 얘기하면서 더 자세히 하겠다.
'STUDY > 자료구조' 카테고리의 다른 글
| [자료구조] stack, queue, sorted list, unsorted list (0) | 2020.10.21 |
|---|---|
| [자료구조] stack, queue, 정렬&비정렬 리스트 시간복잡도 정리 (0) | 2020.10.20 |
| [자료구조] 비정렬 리스트 Array based vs Linked List (0) | 2020.10.18 |
| [자료구조] Queue - Array based vs Linked List (0) | 2020.10.17 |
| [자료구조] stack- Array based vs Linked List (0) | 2020.10.16 |