DP + LCS Algorithm에 대한 이해: 최장 공통 부분 수열 (Longest common subsequence problem)

LCS

: 최장 공통 부분수열 문제

주어진 여러 개의 수열 모두의 부분수열이 되는 수열들 중에 가장 긴 것을 찾는 문제이다.

다시 말해서 두개의 수열 사이에서 가장 긴 공통 부분 수열을 구하는 문제이다.

이때 주의할 점은 substring이 아니라 subsequence 이기 때문에 연속하지 않아도 된다는 것이다.

LCS 풀이 접근 방법

그럼 LCS는 어떻게 구할 수 있을까? 기본 아이디어는 DP를 사용한다.

예를 들어 ACAYKP, CAPCAK 두 문자열의 LCS를 구한다고 해보자.

이때 두 문자열을 하나씩 늘려가면서 비교해가는 방법이 가장 쉬운 접근이다.

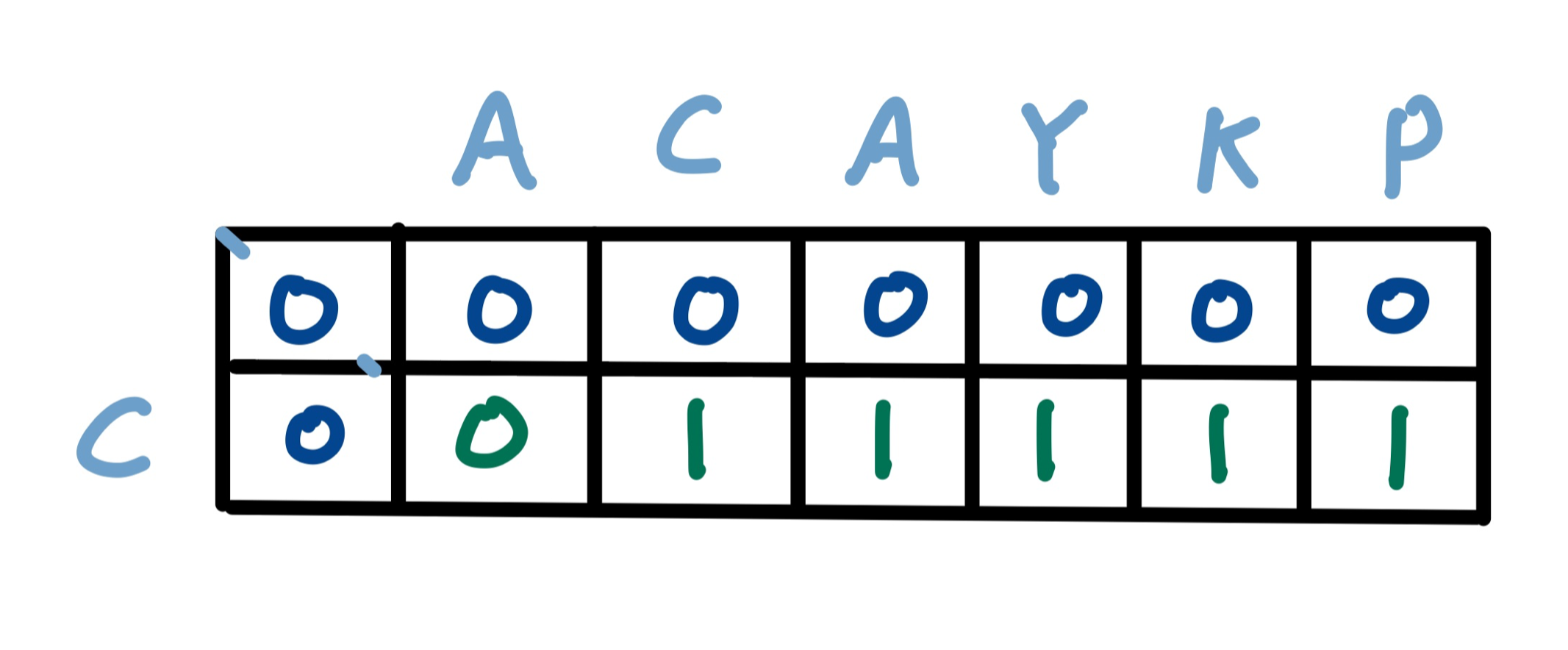
이때 DP를 사용하여 dp 테이블에 값을 저장한다.

문자열 ACAYKP와 두번째 문자열의 첫번째 char인 C와 최장 공통 수열의 길이는 1이다.

이러한 dp 테이블은 다음과 같은 점화식으로 생성한다.

1. 현재 비교하고자 하는 문자가 같으면 공통 부분을 발견한 것이므로 [대각선 값 + 1]

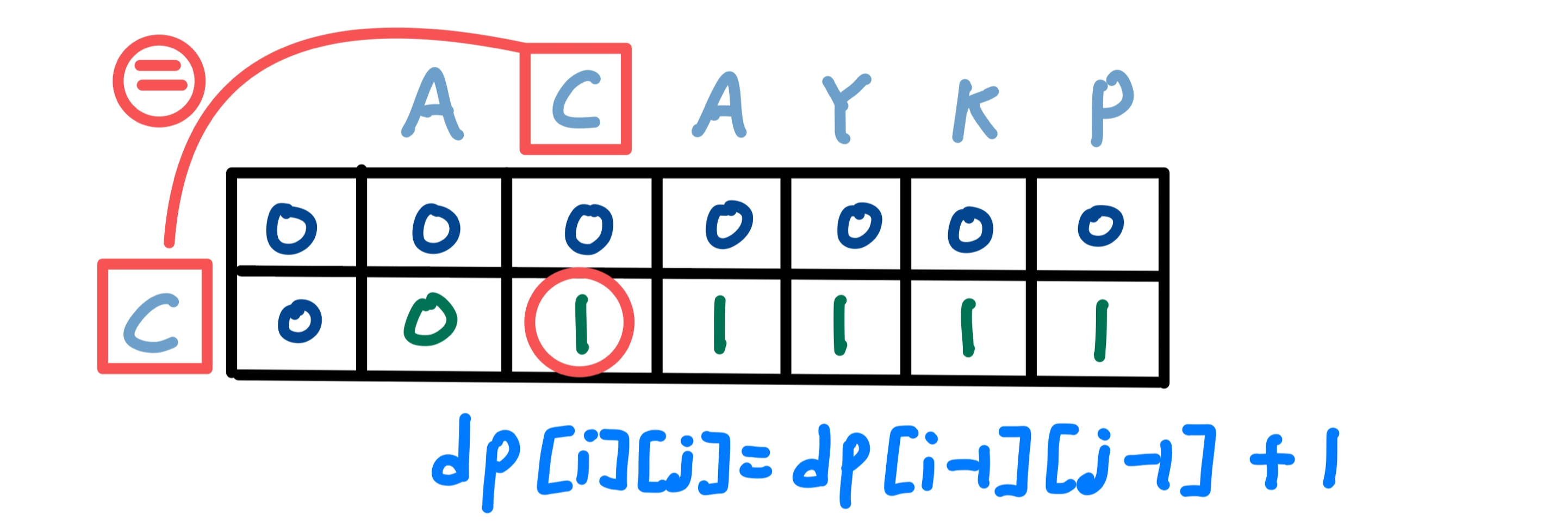
왜냐하면 공통 문자열의 maximum을 구하는 것이기 때문에 이전 대각선의 값에 + 1을 하는 것이다.

이전 대각선의 값에는 현재 문자 이전까지 최장 공통 문자열의 값이 저장되어 있기 때문이다.

이것이 바로 dp의 특성을 이용하는 부분이 된다.

2. 현재 비교하고자 하는 문자가 같지 않으면 이전 값 중 가장 큰 값을 저장한다.

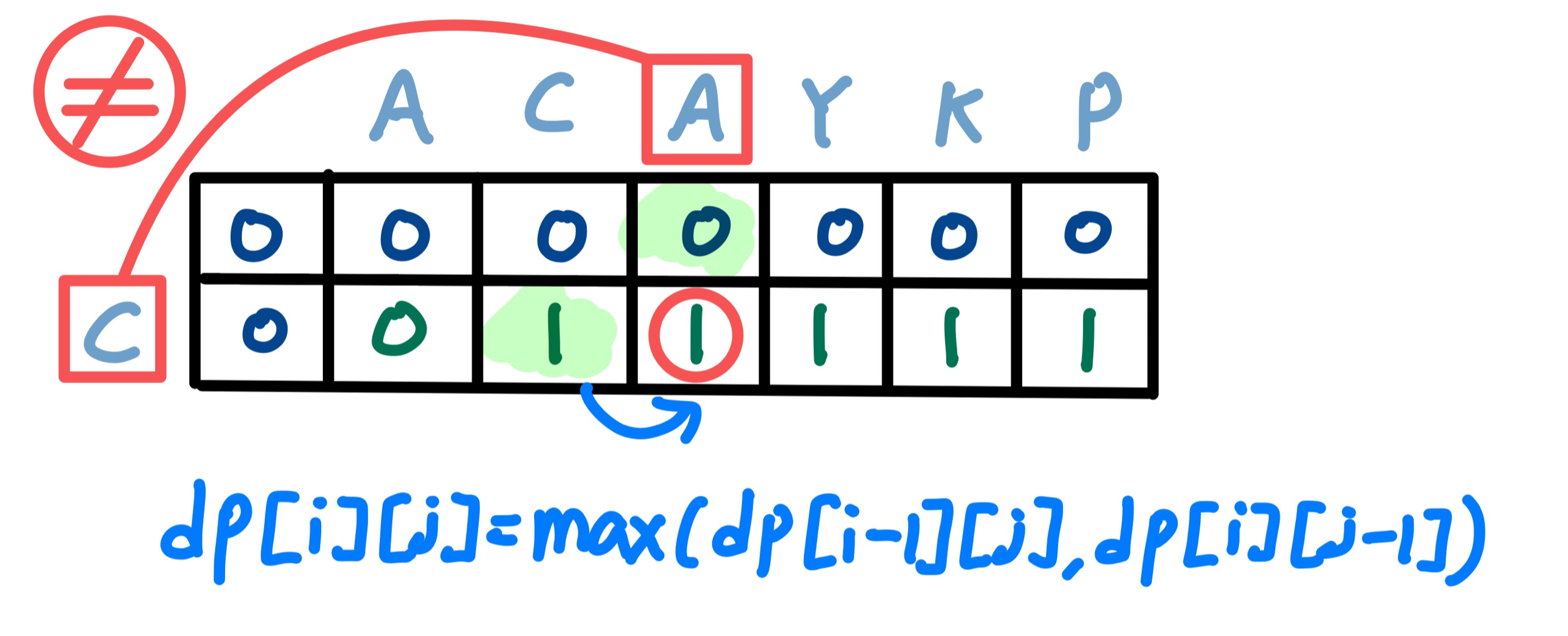
이때 말하는 이전 값이라는 것은 현재 문자를 포함하기 이전의 LCS 값을 말한다.

예를 들어 위와 같은 경우에서라면 현재 비교하고자 하는 문자인 A와 C가 같지 않다. 따라서 이전에 저장해둔 최장 공통 수열을 가져와서 dp 테이블에 저장해야 한다. 이때 이전에 저장해둔 값은 다음 두가지 경우가 된다.

- ACA 와 비교할게 없는 경우 (0)

- AC와 C를 비교한 경우 (1)

왜냐햐면 현재 비교 문자를 둘 중에 하나씩 제거해야 하기 때문이다.

우리의 목표는 maximum을 구하는 것이다. 따라서 dp 테이블에서 위, 왼쪽 값 중에서 가장 큰 값을 저장하게 된다.

위 점화식으로 두번째 문자에 대해서도 비교하게 되면 다음과 같은 dp 테이블이 형성된다.

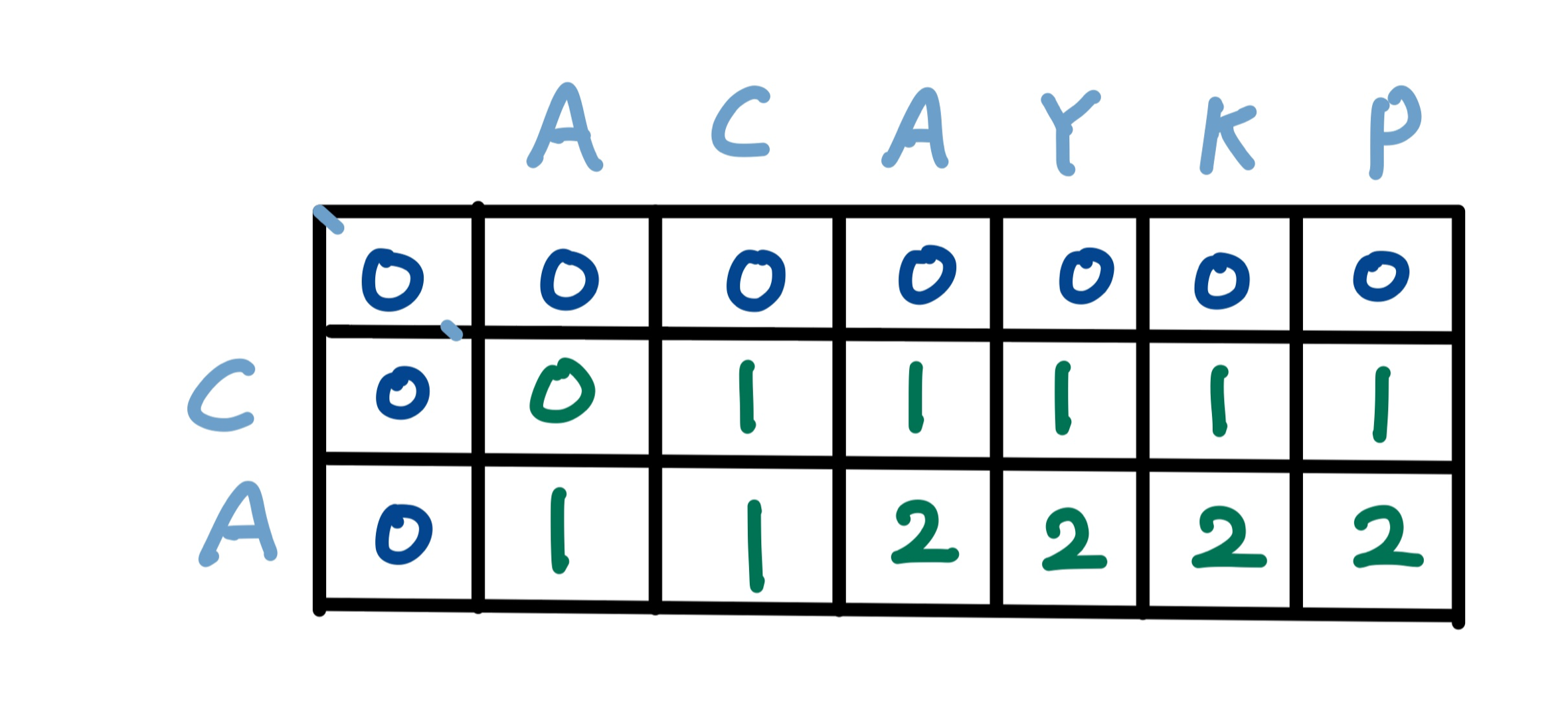
이를 모든 문자에 대해서 비교한다면 결과적으로 다음과 같은 최종 dp 테이블이 생성된다.

최종 테이블을 봤을 때 LCS의 값은 마지막 값이 된다.

즉 LCS는 dp[str1.size()][str2.size()] 에 저장된다.

LCS 점화식 구현

위의 알고리즘을 바탕으로 LCS의 구현은 다음과 같이 이루어진다.

    for(int i = 1;i <= str1.size();i++)
    {
        for(int j = 1;j <= str2.size();j++)
        {
            // 비교 문자 값이 같다면 대각선의 값 + 1
            if (str1[i - 1] == str2[j - 1])
                dp[i][j] = dp[i - 1][j - 1] + 1;
                
           // 값이 다르다면 인접한 값중 큰 값
            else
            {
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    
    // 최종 LCS 답은 dp 테이블의 마지막 칸
    cout<<dp[str1.size()][str2.size()]<<"\n";

LCS를 구성하는 문자열 찾기: 경로 탐색

위와 같이 LCS의 크기를 구하는 문제와 더불어서 최장 공통 수열을 이루는 값을 구하는 문제도 있다.

즉 LCS를 구한 dp 테이블에서 경로를 탐색하는 문제가 된다.

이는 위 LCS 알고리즘을 이해했다면 아주 간단하다.

다음과 같은 과정으로 탐색을 하게 된다.

1. 경로 탐색은 LCS의 값을 저장하는 dp 테이블의 마지막 칸에서 시작한다.

왜냐하면 마지막 칸이 LCS 값이므로 이 값이 어디서 왔는지 추적하면 공통 문자도 구할 수 있기 때문이다.

2. 현재 칸과 인접한 칸 중에서 같은 값을 가진 칸이 있다면 그 칸으로 이동한다.

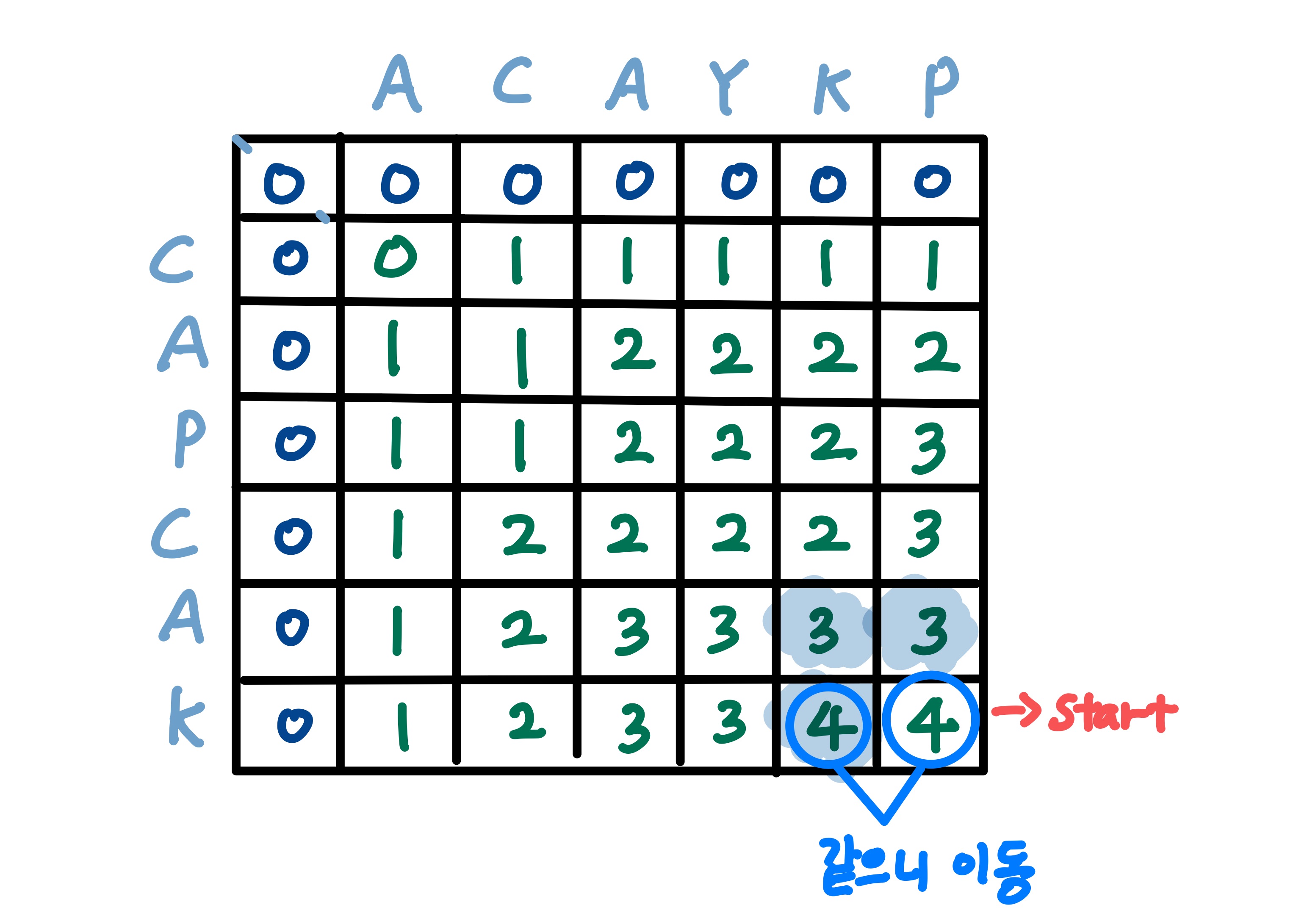
이전에 LCS를 구할 때의 알고리즘을 다시 떠올려보자.

비교하고자 하는 문자가 같지 않으면 위쪽, 왼쪽 칸 중에서 가장 큰 값을 저장한다.

위와 같은 점화식 규칙이 생각난다면 90퍼 정도 이해한 것이다.

위 점화식 규칙을 반대로 생각해보면

현재 보고 있는 칸의 값이 위쪽, 왼쪽 칸과 같은 값이라면 이는 비교하고자 하는 문자가 같지 않다는 뜻이 된다.

따라서 LCS를 구성하는 문자가 아니라는 뜻이므로 배열에 저장하지 않고 이동만 하게 되는 것이다.

3. 현재 칸과 인접한 칸 중에서 같은 값을 가진 칸이 없다면, 현재 칸의 문자를 경로 배열에 저장하고 대각선으로 이동한다.

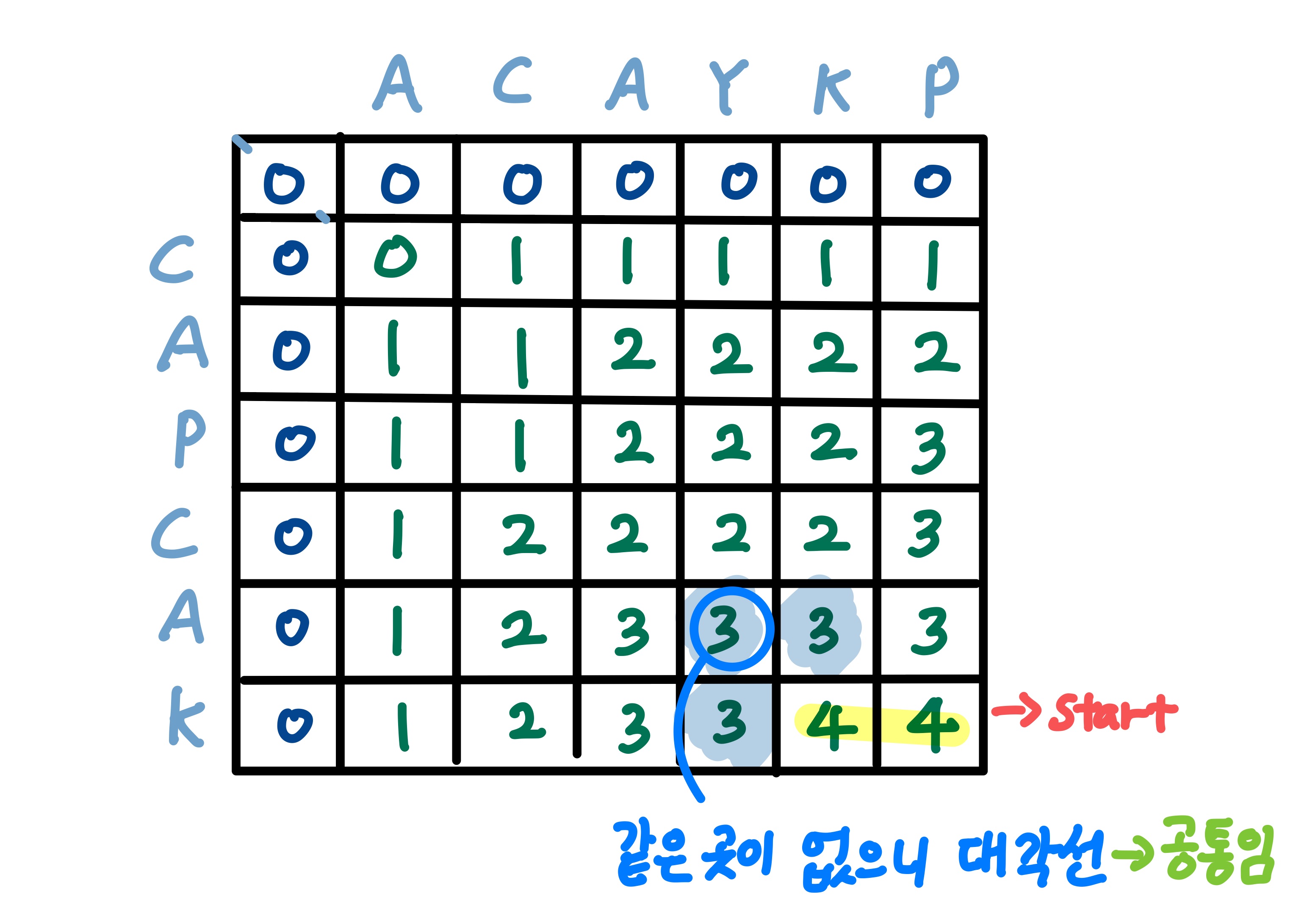
위와 같은 방법으로 이전에 LCS를 구할 때의 알고리즘을 다시 떠올려보자.

비교하고자 하는 문자가 같다면, [대각선의 값 + 1] 을 저장한다.

위 점화식 규칙을 반대로 생각해보면

위쪽, 왼쪽 칸의 값과 현재 보고 있는 칸의 값이 같지 않다면, 이는 현재 칸의 문자가 공통 문자가 된다는 뜻이 된다.

따라서 현재 칸의 문자를 경로 배열에 저장하고, 대각선에서 왔기 때문에 이번에는 반대로 대각선으로 이동한다.

4. i 또는 j가 0이 되면 탐색을 종료한다.

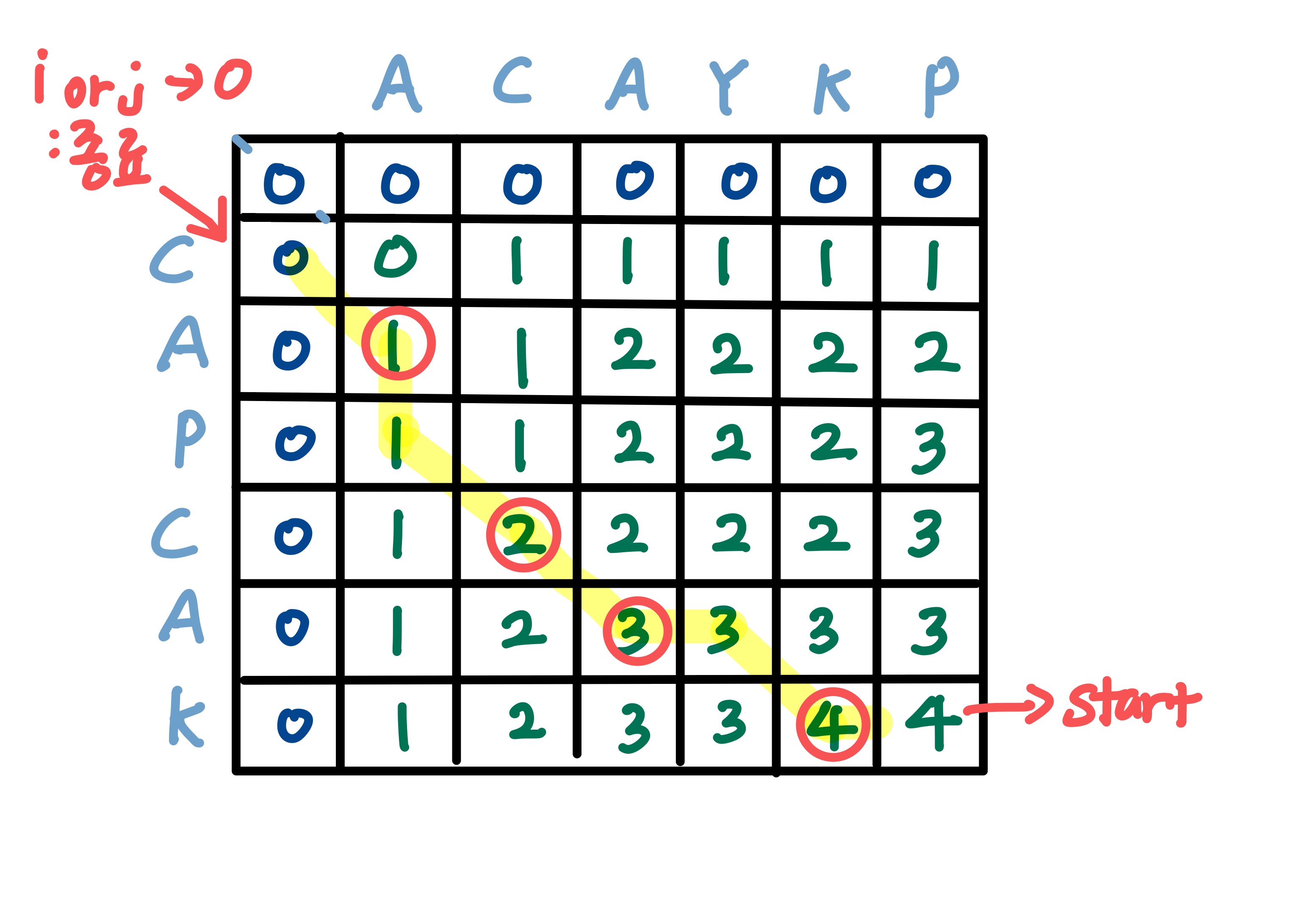
탐색 종료 조건은 행 또는 열이 0이 되는 것이다.

이때 경로 배열에 저장된 문자를 보면 K, A, C, A 일 것이다.

이는 거꾸로 된 값이므로 배열을 뒤집어서 출력하면 최종 LCS 경로가 된다.

예시 문제

BOJ 9251: LCS
BOJ 9252: LCS2
BOJ 5582: 공통 부분 문자열
leetcode 583: Delete Operation for Two Strings

백준 9251: LCS

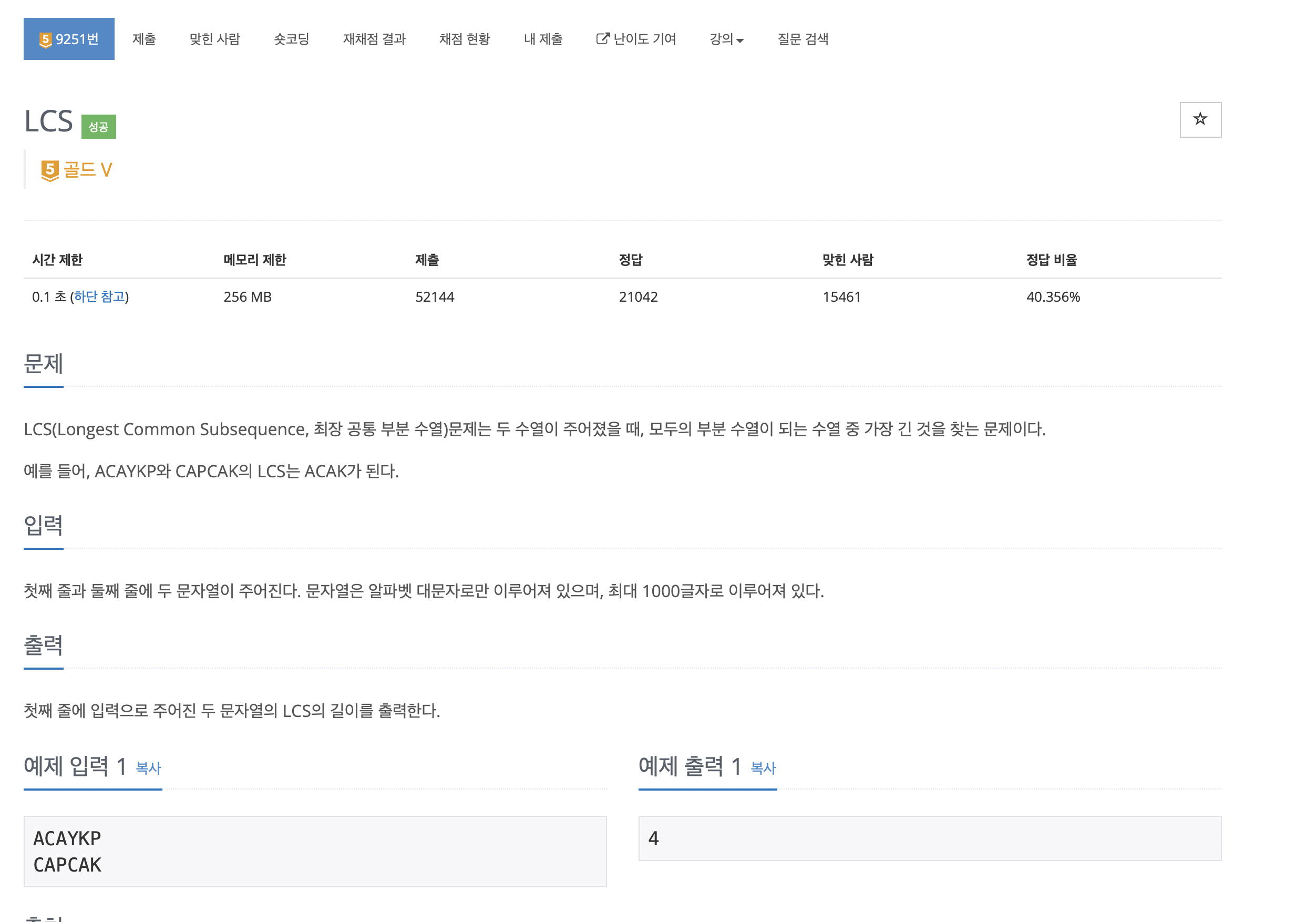
아이디어: LCS

가장 기본적인 LCS 문제이다. 위의 알고리즘 기본 개념대로 dp를 적용해서 쉽게 풀 수 있다.

구현

#include <string>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;

int dp[1001][1001];
int main()
{
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(false);
    
    string str1, str2;
    cin>>str1>>str2;
    
    for(int i = 1;i <= str1.size();i++)
    {
        for(int j = 1;j <= str2.size();j++)
        {
            if (str1[i - 1] == str2[j - 1])
                dp[i][j] = dp[i - 1][j - 1] + 1;
            else
            {
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    cout<<dp[str1.size()][str2.size()]<<"\n";
    
    return 0;
}

백준 9252: LCS2

아이디어: LCS + 경로

이 또한 기본 LCS 문제이다. 9251과 다른 점은 경로를 저장해야 한다는 것이고, 위에서 설명한 알고리즘 개념대로 쉽게 풀 수 있다.

구현

#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
#include <queue>
using namespace std;

int main()
{
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(false);

    string s1, s2;
    cin>>s1>>s2;
    
    vector<vector<int>> dp(s1.size() + 1, vector<int>(s2.size() + 1, 0));
    for(int i = 1;i <= s1.size();i++)
    {
        for(int j = 1;j <= s2.size();j++)
        {
            if (s1[i - 1] == s2[j - 1])
                dp[i][j] = dp[i - 1][j - 1] + 1;
            else
                dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);
        }
    }
    vector<char> res;
    queue<pair<int, int>> q;
    q.push({s1.size(), s2.size()});
    
    // 경로 탐색
    while(!q.empty())
    {
        int x = q.front().first;
        int y = q.front().second;
        
        q.pop();
        
        if (x == 0 || y == 0)
            break;
        
        if (dp[x - 1][y] == dp[x][y])
        {
            q.push({x - 1, y});
        }
        
        else if (dp[x][y - 1] == dp[x][y])
        {
            q.push({x, y - 1});
        }
        
        else
        {
            res.push_back(s1[x - 1]);
            q.push({x - 1, y - 1});
        }
        
    }
    
    cout<<dp[s1.size()][s2.size()]<<"\n";
    for(int i = res.size() - 1;i >= 0;i--)
        cout<<res[i];
    cout<<"\n";
    
    return 0;
}

백준 5582: 공통 부분 문자열

아이디어: LCS 응용

이 문제는 기본 LCS와 다르게 "연속된" 공통 문자열을 찾는 것이 핵심이다. 따라서 기존 LCS 알고리즘에서 응용을 해야한다.

연속으로 존재하는 공통 문자열 중 가장 긴 길이를 구하는 것이므로 공통인 부분이 끝나게 되면 그 뒤에서 찾는 것을 종료하면 된다.

즉 비교하는 문자가 같지 않을 때는 dp 값을 0으로 만들어주면 되는 것이다.

구현

#include <string>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;

int main()
{
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(false);
    
    string str1, str2;
    cin>>str1>>str2;
    
    vector<vector<int>> dp(str1.size() + 1, vector<int>(str2.size() + 1, 0));
    
    for(int i = 1;i <= str1.size();i++)
    {
        for(int j = 1;j <= str2.size();j++)
        {
            if (str1[i - 1] == str2[j - 1])
                dp[i][j] = dp[i - 1][j - 1] + 1;
                
            // 비교하는게 같지 않으면 0으로 만들어줌.
            else
                dp[i][j] = 0;
        }
    }
    
    // dp 테이블 중에서 최장 길이 구하기
    int result = 0;
    for(int i = 1;i <= str1.size();i++)
    {
        for(int j = 1;j <= str2.size();j++)
        {
            result = max(result, dp[i][j]);
        }
    }
    
    cout<<result<<"\n";
                               
    return 0;
}

leetcode 583 Delete Operation for Two Strings

아이디어: LCS

문제에서 구현해야 하는 것은 두개의 문자열을 같게 만들기 위한 최소 연산의 수다.

이를 위해서는 몇개의 문자가 공통으로 존재하는지, 즉 공통 부분 수열을 구해야 하는데 연산의 수가 최소가 되어야 하므로 공통 부분 수열은 최대가 되어야 한다.

따라서 DP와 함께 LCS 알고리즘을 적용할 수 있다.

구현

// 문제 핵심 접근: 중복되는 가장 긴 문자열 찾기

class Solution {
public:
    int minDistance(string word1, string word2) {
	
    	// DP table
        vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));
        
        for(int i = 1;i <= word1.size();i++)
        {
            for(int j = 1;j <= word2.size();j++)
            {
                if (word1[i - 1] == word2[j - 1])
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                else
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
        return word1.size() + word2.size() - dp[word1.size()][word2.size()] * 2;

    }
};

참고

최장 공통 부분 수열 - 위키백과, 우리 모두의 백과사전

최장 공통 부분수열 문제는 LCS라고도 불린다. 이는 주어진 여러 개의 수열 모두의 부분수열이 되는 수열들 중에 가장 긴 것을 찾는 문제다.(종종 단 두 개중 하나가 되기도 한다.) 컴퓨터 과학에

ko.wikipedia.org

'ALGORITHM > c&c++ baekjoon' 카테고리의 다른 글

[C++/11559] puyo puyo - using simulation (0)	2023.08.15
[C++/14502] 연구소 - using BFS (0)	2023.01.09
음수 간선을 가지는 그래프의 최단 경로: 벨만-포드 알고리즘 (0)	2022.05.20
[C++/1697, 11779] 탐색 중 이전 값를 저장해야 하는 유형의 문제들 (0)	2022.05.17
[C++/3665] 최종 순위 - using 위상 정렬 (topology sort) (0)	2022.05.14

컴공에서 살아남기